31

Wenn man den inneren roten Kreis (der genau halb so viel im Durchmesser misst wie der blaue) im blauen Kreis abrollen lässt, welche Bahn beschreibt dann der schwarze Punkt?

32

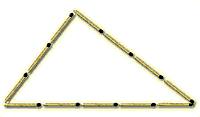Durch hinzufügen von 2 Streichhölzern soll man bei dieser Figur die Fläche des Dreiecks genau halbieren. Die beiden Hölzer sind so zu legen, dass jeweils nur Streichholzenden oder -köpfe der Streichhölzer einander berühren.

33

"Hey Chef!", meint der Lehrling beim Montieren von Seriennummerschildchen an Waschmaschinen, wir sollten wohl einen andern Schriftsatz verwenden in Zukunft und nicht mehr diesen hier.

Ich habe nämlich hier eben ein Schildchen gefunden, mit einer 5 Stelligen Nummer drauf, das man sowohl normal wie auch um 180° gedreht lesen kann, wobei alle Ziffern innerhalb der Zahl verschieden sind. Darauf der Chef: "Oh! Das habe ich noch gar nie bemerkt Du hast recht! Der Chef dreht das Schildchen ein paar mal hin und her meint dann: "Hmm, also Du musst das so rum montieren, denn um 180° gedreht wäre die Zahl sonst um 7920 zu hoch!"

Welche Nummer steht auf dem Schildchen?

34

Unterteile ein x-beliebiges Quadrat in 6 kleinere Quadrate ohne dass etwas übrig bleibt!

35

Neun Münzen sind in einem Quadrat zu 3 x 3 Münzen hingelegt. Wenn man nun gerade Linien durch jeweils 3 Münzen zieht, kommt man auf 8 Linien. Durch Umlegen von 2 Münzen kann man nun erreichen, dass man 10 gerade Linien durch jeweils 3 Münzen ziehen kann.

Wie schafft man das?

36

Für welche verschiedenen Ziffern stehen X, Y und Z bei folgender Rechnung?

XZY + XYZ = YZX

37

Klaus und Peter möchten 2 kg Zucker abwiegen. Sie haben aber nur eine Balkenwaage mit zwei ungleich langen Armen, ein 1 kg Gewicht, ein paar Tüten und genügend Zucker.

Wie sollen Klaus und Peter vorgehen?

38

Eine sehr knifflige Angelegenheit. Die folgende Figur ist durch zwei gerade Schnitte so in vier Teile zu zerlegen, dass man aus diesen vier Teilen ein Quadrat zusammenfügen kann. Wie sehen dies zwei Schnitte aus?

39

Hier sieht man eine Schaufel aus 5 Zündhölzern.

Durch das Verschieben von zwei Zündhölzern kriegt man wieder eine Schaufel, diesmal liegt der Schmutz aber ausserhalb der neuen Schaufel.

40

In einer Strasse stehen fünf Häuser unterschiedlicher Farbe. Sie werden von fünf Männern verschiedener Nationalität bewohnt. Jeder der Männer hat in Bezug auf Rauchen, Trinken und Haustiere andere Gewohnheiten.

Häuser (1, 2, 3, 4, 5)
Farbe (gelb, weiss, rot, grün, blau)
Nationalität (Norwegen, England, Spanien, Holland, Japan)
Rauchen (Zigaretten, Zigarren, Filter, Pfeife, Zigarillo)
Trinken (Milch, Orangensaft, Kaffee, Wasser, Tee)
Haustiere (Hund, Pferd, Fuchs, Schnecke, Zebra)

Hinweise
1.   Der Engländer lebt in dem Haus mit der roten Türe.
2.   Der Spanier hat einen Hund.
3.   Kaffe wird in dem Haus mit der grünen Türe getrunken.
4.   Der Holländer trinkt Tee.
5.   Das Haus mit der grünen Türe befindet sich direkt neben dem Haus mit der weissen Türe.
6.   Im Haus mit der gelben Türe werden Zigaretten geraucht.
7.   Der Zigarilloraucher hält sich Schnecken.
8.   Der Norweger lebt neben dem Haus mit der blauen Türe.
9.   Milch wird im mittleren Haus getrunken.
10. Der Norweger lebt im ersten Haus links.
11. Der Mann, der die Filterzigaretten raucht, lebt in dem Haus, welches neben dem Mann mit dem Fuchs liegt.
12. Zigarette wird geraucht im Haus, das neben dem Haus liegt, in dem man das Pferd hat.
13. Der Zigarrenraucher trinkt Orangensaft.
14. Der Japaner raucht Pfeife.

Frage
Wer trinkt Wasser und wem gehört das Zebra?