Dreieck berechnen

Ein Dreieck kann eindeutig konstruiert werden, wenn eine dieser Kombinationen an gegebenen Massen vorliegt:
- eine Seite und zwei Winkel (SWW, WSW oder WWS)
- zwei Seiten und der der grösseren Seite gegenüberliegende Winkel (SSW oder WSS)
- zwei Seiten und der eingeschlossene Winkel (SWS)
- drei Seiten (SSS)
Drei Werte sind einzugeben. Der Rest wird berechnet.
Bei Dezimal-Eingabe ist der Punkt zu verwenden.
Jede Längeneinheit kann gewählt werden, es muss aber immer die gleiche sein.
- eine Seite und zwei Winkel (SWW, WSW oder WWS)
- zwei Seiten und der der grösseren Seite gegenüberliegende Winkel (SSW oder WSS)
- zwei Seiten und der eingeschlossene Winkel (SWS)
- drei Seiten (SSS)
Die Fläche eines Dreiecks kann auch mit der Heron's Formel berechnet werden.
Drei Werte sind einzugeben. Der Rest wird berechnet.
Bei Dezimal-Eingabe ist der Punkt zu verwenden.
Jede Längeneinheit kann gewählt werden, es muss aber immer die gleiche sein.
Die Formeln
Beliebiges Dreieck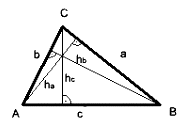 |
Rechtwinkeliges Dreieck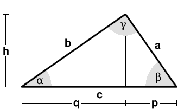 |
|
Satz des Pythagoras |
||
|
Höhensatz |
||
| Kathetensatz |
||
Gleichseitiges Dreieck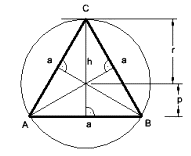 |
Umkreisradius (gilt für jedes Dreieck)
|
Inkreisradius (gilt für jedes Dreieck)
|
Cosinussatz
a = √ (b2 + c2 - 2 b c cos α)
b = √ (a2 + c2 - 2 a c cos β)
c = √ (a2 + b2 - 2 a b cos γ)
Aufgelöst nach Winkeln
α = arccos [(-a2 + b2 + c2)/(2 b c)]
β = arccos [(-b2 + a2 + c2)/(2 a c)]
γ = arccos [(-c2 + a2 + b2)/(2 a b)]
arccos [ ] = arctan √[(1 - X2)/X], wobei ist X = cos [ ]
Sinussatz
a / sin α = b / sin β = c / sin γ
Satz der Winkelsumme
α + β + γ = 180
Umrechnung von Grad (°) in Bogenmass (radians)
Grad = Bogenmass (180 / 3,141593)
Bogenmass = Grad (3,141593 / 180)
